PGS.TS. Đinh Hồng Dương
Mở đầu
Mục đích
Đo lường tần số mắc bệnh và chết ở cộng đồng là để mô tả thực trạng sức khỏe cộng đồng, làm cơ sở cho việc lập kế hoạch chăm sóc sức khỏe cũng như đánh giá hiệu quả của các can thiệp y tế dự phòng. Đồng thời nó cũng là cơ sở cho các nghiên cứu phân tích dịch tễ học nhằm xác định yếu tố nguy cơ của dịch bệnh.
Số đo
Số đo tuyệt đối
Là số liệu thô, thể hiện độ lớn của sự kiện quan sát mà không xem xét đến độ lớn của quần thể, nơi sự kiện đó xảy ra.
Ví dụ: Số người mắc thương hàn ở tỉnh A năm 2000: 1200 người. Số người chết do tai nạn giao thông tháng 2/2000 ở thành phố H: 45 người.
Số đo tương đối
Là số đo, trong đó độ lớn của sự kiện quan sát đã được đặt trong mối tương quan với độ lớn của quần thể nơi sự kiện đó xảy ra dưới dạng tỷ số, tỷ lệ, tỷ suất.
Chỉ số mắc bệnh
Tỷ lệ hiện mắc (prevalence – p)
Là tỷ lệ giữa số người có bệnh ở một quần thể trên tổng dân số của quần thể tại một thời điểm hoặc thời khoảng xác định.
Công thức:
Tổng số người có bệnh ở một quần thể
P = ————————————————————————— x k
Tổng dân số của quần thể tại thời điểm hoặc thời khoảng
Nếu tử số là số các trường hợp đang mắc bệnh được phát hiện qua một nghiên cứu ngang ở một thời điểm nhất định còn mẫu số là tổng dân số của quần thể ở thời điểm đó, ta sẽ có tỷ lệ hiện mắc điểm (point prevalence). – Nếu tử số là số các trường hợp đang mắc bệnh được phát hiện qua một theo dõi dọc trong một khoảng thời gian xác định (6 tháng, 1 năm hoặc dài hơn). Mẫu số là dân số trung bình của quần thể trong khoảng thời gian đó, ta sẽ có tỷ lệ hiện mắc kỳ (period prevalence).
Việc tính dân số trung bình trong một khoảng thời gian dài nhiều năm với quần thể nhỏ không khó. Tuy nhiên, nếu quần thể lớn (ví dụ 1 tỉnh với dân số hàng triệu người) sẽ khó tính chính xác dân số trung bình. Trường hợp này, người ta cho phép ước lượng dân số trung bình bằng cách lấy trung bình dân số ở thời điểm bắt đầu quan sát và thời kết thúc quan sát hoặc lấy dân số ở thời điểm giữa của cuộc quan sát.
Hệ số k là bội số của 10 (kn) với n từ 1 – 5. Việc sử dụng hệ số k với 2 mục đích:
Với các tỷ lệ nhỏ, tăng hệ số k để đảm bảo các tỷ lệ là 1 số nguyên, dương có nghĩa.
Sử dụng hệ số k để các tỷ lệ có cùng mẫu số sẽ rất có lợi khi so sánh các tỷ lệ ở cùng một quần thể hoặc giữa các quần thể khác nhau.
Ví dụ: Xã A ở Tây Nguyên có 3000 dân. Tháng 3/2000 có 75 bệnh nhân sốt rét. Tỷ lệ hiện mắc sốt rét điểm của xã A: P điểm = 75/3000 hay 25/1000 dân (k =3).
Tỷ lệ mới mắc (incidence – i)
Tỷ lệ mới mắc là tỷ lệ giữa tổng số người mới mắc bệnh trong một khoảng thời gian ở một quần thể trên tổng dân số có nguy cơ mắc bệnh của quần thể trong khoảng thời gian đó. Tỷ lệ mới mắc chỉ có thể phát hiện được trong một theo dõi dọc.
Tỷ lệ mới mắc tích lũy (Cumulative Incidence – CI)
Công thức:
Tổng số người mới mắc bệnh của một quần thể
CI = ———————————————————————— x k
Tổng dân số của quần thể đó tại thời điểm bắt đầu quan sát
Tử số là số các trường hợp mới mắc bệnh được phát hiện trong khoảng thời gian quan sát. Có nghĩa là tử số chỉ quan tâm đến các trường hợp có thời điểm mắc bệnh nằm trong khoảng thời gian quan sát mà không cần quan tâm đến thời điểm kết thúc bệnh (bằng khỏi hoặc chết).
Mẫu số về lý thuyết là tổng dân số có nguy cơ của quần thể đó trong khoảng thời gian quan sát. Tuy nhiên, với các quần thể lớn (một tỉnh hoặc một quốc gia) không thể tính chính xác dân số trung bình, nên thường lấy tổng dân số ở thời điểm bắt đầu quan sát hoặc ở thời điểm giữa của khoảng thời gian quan sát.
Hệ số k tương tự như tỷ lệ hiện mắc.
Một số lưu ý về tỷ lệ mới mắc tích lũy:
Thời gian theo dõi: thường là 1 năm, nhưng cũng có thể dài hoặc ngắn hơn. Nói chung, khoảng thời gian đó phải đủ dài để có thể đảm bảo sự ổn định của tử số. Ví dụ: nếu một bệnh có chu kỳ thì thời gian theo dõi phải ít nhất kéo dài bằng chu kỳ đó là chính xác nhất (thời gian theo dõi là bội số của một chu kỳ, nếu chu kỳ là 3 năm thì có thể theo dõi trong 3; 6; 9 năm đều được). Nếu theo dõi ngắn hơn một chu kỳ thì tỷ lệ mới mắc có thể thấp hơn thực tế nếu khoảng thời gian theo dõi rơi vào chu kỳ thấp và ngược lại, tỷ lệ mới mắc có thể cao hơn thực tế nếu khoảng thời gian theo dõi rơi vào chu kỳ cao của bệnh.
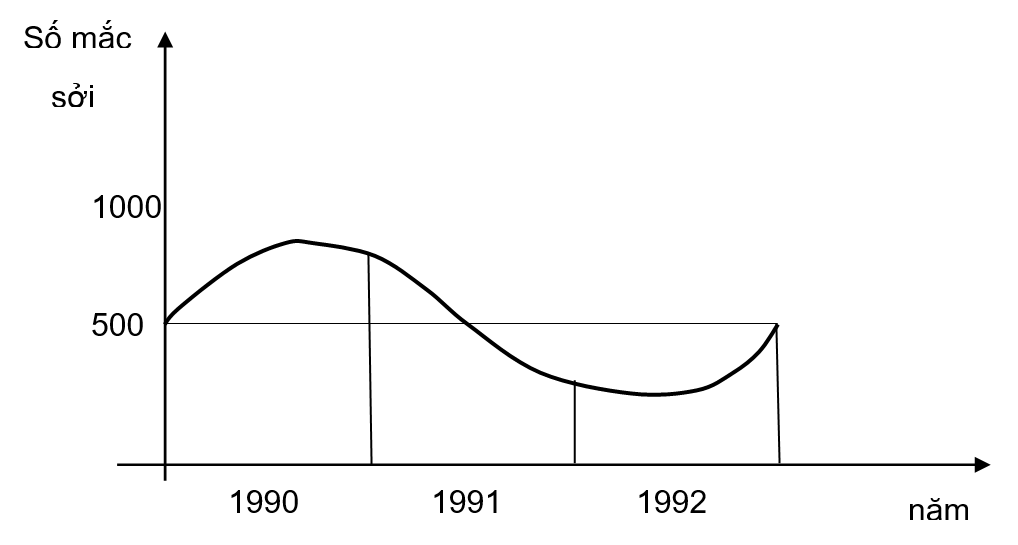
Hình 2.1: Diễn biến bệnh sởi trong 3 năm tại Việt Nam (1990 – 1992)
Theo hình 2.1: Bệnh sởi trước khi đưa vắc xin vào Chương trình tiêm chủng mở rộng thường có chu kỳ 3 năm lại có một vụ dịch. Nếu thời gian theo dõi bệnh sởi trong năm thứ nhất của chu kỳ mắc sởi (1990) thì số mới mắc sởi theo dõi được trong thời gian này cao nhất nên tỷ lệ mới mắc sởi sẽ cao hơn thực tế. Ngược lại, nếu chúng ta theo dõi bệnh sởi vào năm cuối của chu kỳ (1992) thì số mắc sởi theo dõi được sẽ thấp nhất nên tỷ lệ mới mắc sởi sẽ thấp hơn so với thực tế. Chính vì vậy, với những bệnh có chu kỳ (như sởi) thì thời gian theo dõi phải bao phủ cả chu kỳ thì kết quả thu được mới chính xác.
Trong một số bệnh có hơn một lần mắc bệnh với một người trong 1 năm thì ta sẽ có 2 loại tỷ lệ mới mắc bệnh. Ví dụ một người có thể bị cúm nhiều lần trong 1 năm, và nếu thời gian theo dõi là 1 năm thì ta sẽ có 2 tỷ lệ:
Tổng số người mới mắc cúm
(a)Tỷ lệ mới mắc cúm = ——————————————- x k
Tổng dân số của quần thể
Tổng số lần mắc cúm
(b)Số lần bị cúm trung bình = ———————————– x k
Tổng dân số của quần thể
Tỷ lệ thứ nhất (a) cho ta biết xác suất của một người trong quần thể có thể mắc cúm trong 1 năm (ví dụ 2 người/100 dân), còn tỷ lệ thứ hai (b) cho ta ước tính số lần có thể mắc cúm ở quần thể trong một năm là bao nhiêu (ví dụ 3 lần/100 dân).
Tỷ lệ mật độ mới mắc (Incidence Density – ID) (hoặc tỷ suất mới mắc)
Công thức:
Tổng số người mới mắc bệnh của một quần thể
ID= ———————————————————————— năm-người
Tổng số đơn vị thời gian của mỗi cá thể có nguy cơ theo dõi được
Tử số là số các trường hợp mới mắc bệnh được phát hiện trong khoảng thời gian quan sát (tương tự như tỷ lệ mới mắc tích lũy).
Mẫu số về lý thuyết được tính bằng cách: Lấy tổng đơn vị thời gian của toàn bộ quần thể, trừ đi một số đơn vị thời gian bị mất đi do một số cá thể không còn nguy cơ mắc bệnh (do mới bị bệnh; đã chết vì bất kỳ lý do nào; đã chuyển ra khỏi nghiên cứu và không thể theo dõi được).
Ví dụ: Theo dõi 5000 người hút thuốc lá trong 5 năm để đánh giá tình trạng ung thư phổi, cho kết quả: Có một người mắc ung thư phổi sau một năm theo dõi; 5 người chết vì tai nạn giao thông và 3 người chết vì bệnh suy thận sau hai năm theo dõi; 7 người chuyển đi nơi khác sinh sống sau ba năm và không thể tiếp tục theo dõi được; hai người khác mắc ung thư phổi sau 4 năm theo dõi.
Bài giải: Có thể tóm tắt bài toán bằng hình vẽ như sau:
Hình 2.2: Tóm tắt kết quả theo dõi 5000 người trong 5 năm
Theo hình 2: 5000 người sau 5 năm theo dõi có 3 người ung thư phổi. Như vậy tổng số người mới mắc ung thư phổi là 3 (tử số = 3).
Bây giờ ta tìm mẫu số:
Bảng 2.1: Tổng số đơn vị thời gian có nguy cơ của các cá thể theo dõi được
|
TT |
Tình huống |
Tổng số đơn vị thời gian có nguy cơ, theo dõi được |
|
1 |
1 người mắc K phổi sau 1 năm |
1 người x 1 năm = 1 năm |
|
2 |
5 người chết vì TNGT sau 2 năm |
5 người x 2 năm = 10 năm |
|
3 |
3 người chết vì suy thận sau 2 năm |
3 người x 2 năm = 6 năm |
|
4 |
7 người chuyển đi nơi khác sau 3 năm |
7 người x 3 năm = 21 năm |
|
5 |
2 người mắc K phổi sau 4 năm |
2 người x 4 năm = 8 năm |
|
6 |
4982 người không mắc K phổi và theo dõi được trong suốt 5 năm |
4982 người x 5 năm=24.910 năm |
|
|
Cộng |
24.956 năm |
Như vậy, theo bảng 1, tổng số đơn vị thời gian của mỗi cá thể có nguy cơ theo dõi được là 24.956 năm. Như vậy, mẫu số là 24.956
Tỷ lệ mật độ mới mắc (ID) ung thư phổi ở nhóm 5000 hút thuốc lá là:
3
ID = —————- = 0,00012 năm-người
24.956
Điều này có nghĩa là: Theo dõi 1 người hút thuốc lá trong một năm thì xác suất để người này bị K phổi là 0,00012.
Hoặc:
1000 người hút thuốc lá trong 1 năm thì xác suất K phổi là: 1000 x 1 x
0,00012 = 0,12 người
1000 người hút thuốc lá trong 10 năm thì xác suất K phổi là: 1000 x 10 x
0,00012 = 1,2 người
10.000 người hút thuốc lá trong 10 năm thì xác suất K phổi là: 10.000 x
10 x 0,00012 = 12 người
10.000 người hút thuốc lá trong 20 năm thì xác suất K phổi là: = 10.000 x 20 x 0,00012 = 24 người
Tuy nhiên, cách tính trong ví dụ trên cho ta kết quả chính xác nhưng chỉ thực hiện được ở những quần thể nhỏ và thời gian theo dõi ngắn. Ở những quần thể lớn và thời gian theo dõi dài, người ta thường sử dụng công thức ước lượng như sau:
3 3
ID = ————————————-= ——————– ≈ 0,00012 năm-người
5000 + (5000 – 1 – 5 – 3 – 7 – 2) 24.955
——————————————–x 5
2
Liên quan giữa tỷ lệ hiện mắc (P) và tỷ lệ mới mắc (I)
Tỷ lệ hiện mắc (P) của một bệnh trong cộng đồng phụ thuộc vào tỷ lệ mới mắc (I) và thời gian kéo dài trung bình của bệnh đó (gọi là bệnh kỳ). Vì vậy, công thức để thể hiện mối liên quan giữa tỷ lệ hiện mắc và mới mắc của các bệnh có P ≥ 10% như sau:
P
——— = I x D
1 – P
Trong đó: P: Tỷ lệ hiện mắc
I: Tỷ lệ mới mắc
D: Bệnh kỳ
Bệnh kỳ (D) là thời gian mắc bệnh trung bình của một bệnh, tính từ khi bệnh khởi phát đến khi kết thúc bằng khỏi hoặc chết.
Với những bệnh có tỷ lệ hiện mắc thấp (P
P = I x D
Từ công thức nêu trên, để làm giảm tỷ lệ hiện mắc của một bệnh nào đó trong cộng đồng, có thể áp dụng các biện pháp:
Giảm số mới mắc bệnh: bằng cách chống dịch hữu hiệu, cắt đứt đường truyền nhiễm, bảo vệ khối cảm thụ bằng các biện pháp đặc hiệu và không đặc hiệu; nâng cao sức khỏe của cộng đồng.
Giảm bệnh kỳ: Cải tiến biện pháp điều trị, nghiên cứu thuốc mới để có thể rút ngắn thời gian điều trị.
Áp dụng đồng thời cả hai biện pháp trên.
Chỉ số chết
Cùng với chỉ số mắc bệnh, chỉ số chết rất quan trọng trong phản ánh thực trạng sức khỏe cộng đồng.
Tỷ lệ chết thô (crude death rate – cdr)
Công thức:
Tổng số người chết vì mọi nguyên nhân
CDR= ————————————————————————- x k
Tổng dân số của quần thể trong thời gian quan sát
Tử số là số chết vì mọi nguyên nhân. Mẫu số là dân số trung bình của quần thể. K là bội số của 10.
Ví dụ: Năm 2000, cộng đồng A có 100.000 dân, có 300 người chết vì mọi nguyên nhân. Tỷ lệ chết thô CDR = 300/100.000.
Tỷ lệ chết đặc hiệu (specific death rate – sdr)
Công thức:
Tổng số người chết vì một nguyên nhân
SDR= ————————————————————– x k
Tổng dân số của quần thể trong thời gian quan sát
Tử số là số chết vì một nguyên nhân. Mẫu số là dân số trung bình của quần thể. K là bội số của 10.
Ví dụ: Năm 2000, cộng đồng A có 100.000 dân, có 300 người chết vì mọi nguyên nhân, trong đó có 20 người chết do bệnh lao. Tỷ lệ chết đặc hiệu với bệnh lao SDR = 20/100.000
Tỷ lệ chết chung và tỷ lệ chết riêng phần
Khi tỷ lệ chết đặc hiệu được tính chung cho toàn bộ quần thể nghiên cứu mà không xem xét tới bất kỳ đặc trưng nào, ta sẽ có tỷ lệ chết chung (chính là tỷ lệ chết đặc hiệu).
Ví dụ: Năm 2000, cộng đồng A có 100.000 dân, có 300 người chết vì mọi nguyên nhân, trong đó có 20 người chết do bệnh lao. Tỷ lệ chết chung với bệnh lao (cũng là tỷ lệ chết đặc hiệu với bệnh lao) là 20/100.000
Khi tỷ lệ chết đặc hiệu được tính riêng theo một hoặc nhiều đặc trưng nhất định (tuổi, giới, dân tộc, tình trạng kinh tế xã hội, nghề nghiệp, thói quen, phong tục tập quán…) ta có tỷ lệ chết riêng phần theo các đặc trưng đó. Ví dụ: Năm 2000, cộng đồng A có 100.000 dân gồm 51.000 nam và 49.000 nữ, có 300 người chết vì mọi nguyên nhân, trong đó có 20 người chết do bệnh lao gồm 8 nữ và 12 nam.
Tỷ lệ chết riêng phần với bệnh lao theo giới là:
Tỷ lệ chết riêng phần với bệnh lao theo nam giới = 12/51.000
Tỷ lệ chết riêng phần với bệnh lao theo nữ giới = 8/49.000
Tỷ lệ chết trên mắc (case fatality rate – cfr)
Công thức:
Tổng số người chết vì một loại bệnh tật
CFR= —————————————————– x k
Tổng trường hợp mắc bệnh đó trong quần thể
Tử số là tổng số chết vì một loại bệnh tật nào đó. Mẫu số là tổng số các trường hợp mắc bệnh đó.
Ví dụ: Năm 2000, cộng đồng A có 100.000 dân gồm 51.000 nam và 49.000 nữ, có 300 người chết vì mọi nguyên nhân, trong đó có 20 người chết do bệnh lao. Số mắc lao của cộng đồng này là: 1120 người. Tỷ lệ chết trên mắc CFR = 20/1120 (1,8%).
Kỹ thuật chuẩn hóa tỷ lệ
Trong nghiên cứu dịch tễ học, nếu các tỷ lệ không được chuẩn hóa, có thể sẽ tạo ra kết quả sai lệch. Từ những kết quả này sẽ dẫn chúng ta đến những hành động, những biện pháp dự phòng sai lầm, đôi khi rất tai hại. Bất kỳ tỷ lệ nào cũng cần được chuẩn hóa. Các tỷ lệ này, về lý thuyết, phải được chuẩn hóa theo tất cả các đặc trưng. Tuy nhiên, đặc trưng tuổi là quan trọng nhất trong các đặc trưng về con người. Vì vậy, nội dung phần này sẽ giới thiệu kỹ thuật chuẩn hóa theo tuổi (các đặc trưng khác đều có kỹ thuật tương tự).
Ví dụ: Tỷ lệ chết chung do ung thư các loại ở Mỹ năm 1940: 120,2/100.000 dân và năm 1980: 183,8/100.000 dân. Thoạt nhìn, rõ ràng có sự gia tăng tỷ lệ chết vì ung thư các loại ở Mỹ một cách rất đang lo ngại, rất đáng báo động. Chỉ trong vòng 40 năm (1940 – 1980), tỷ lệ này đã tăng từ 120,2 lên đến 183,8 (tăng 53%). Nhưng sự thật là: Cấu trúc về tuổi của dân Mỹ đã thay đổi rất đáng kể. Nếu như năm 1940, dân số Mỹ từ 65 tuổi trở lên chỉ chiếm 6,9% (trong tổng số 138,9 triệu người), thì đến năm 1980, con số này tới 11,3% (trong tổng số 226.6 triệu người). Cho nên, sự gia tăng này là do phần cấu trúc tuổi của dân số Mỹ tạo ra, chứ không phải là xu thế gia tăng thực sự của bệnh (tuổi càng cao thì tỷ lệ ung thư càng cao).
Và khi thực hiện kỹ thuật chuẩn hóa tỷ lệ, người ta đã xác định được tỷ lệ chết vì ung thư các loại ở Mỹ năm 1980 không phải là 183,8, mà là 126,2, nghĩa là chỉ tăng 5% ([126,2 – 120,2]/120,2) chứ không phải 53% như quan sát ban đầu. Như vậy, tỷ lệ này chỉ thực sự tăng 5% trong vòng 40 năm.
Người ta đã giải thích sự gia tăng này, ngoài lý do cấu trúc tuổi, còn một số lý do khác:
Do hút thuốc lá nhiều hơn (cả về tỷ lệ và số lượng thuốc hút mỗi ngày);
Có các kỹ thuật chẩn đoán tiên tiến hơn, có thể phát hiện bệnh ung thư nhanh và triệt để hơn;
Các dịch vụ y tế có sẵn hơn và tốt hơn;
Và: Tự người dân quan tâm tới sức khỏe bản thân nhiều hơn.
Như vậy: Chuẩn hóa tỷ lệ là rất cần thiết và quan trọng. Có 2 kỹ thuật là chuẩn hóa trực tiếp và gián tiếp. Chuẩn hóa gián tiếp sẽ không đề cập trong bài học này vì đòi hỏi nhiều điều kiện phức tạp hơn nhiều so với chuẩn hóa trực tiếp.
Kỹ thuật chuẩn hóa trực tiếp có 3 phương pháp:
Lấy một quần thể trong hai quần thể muốn đem so sánh làm chuẩn;
Lấy một quần thể giả định (là tổng của 2 quần thể muốn đem so sánh) làm chuẩn;
Lấy một quần thể thứ ba (khác với hai quần thể muốn đem so sánh) làm chuẩn. Quần thể thứ 3 này có được thông qua một cuộc điều tra dân số và được coi là chuẩn.
Cả ba phương pháp trên đều có cách tính giống nhau, chỉ khác nhau ở quần thể đem ra làm chuẩn. Dưới đây là ví dụ về phương pháp chuẩn hóa thứ nhất (lấy một quần thể trong 2 quần thể muốn đem so sánh làm chuẩn).
Ví dụ: Khi nghiên cứu về mối quan hệ giữa chết vì xơ gan với uống rượu ở hai quần thể: Quần thể A là quần thể người có uống rượu và quần thể B là quần thể người không uống rượu, ta có bảng sau:
Bảng 4.1: Số chết vì xơ gan ở hai quần thể A và B theo nhóm tuổi
|
Nhóm tuổi |
Quần thể A (có uống rượu) |
Quần thể B (không uống rượu) |
||||
|
Số chết |
Số dân |
Tỷ lệ chết (%) |
Số chết |
Số dân |
Tỷ lệ chết (%) |
|
|
20 – 29 |
5 |
100 |
5,0 |
20 |
500 |
4,0 |
|
30 – 39 |
5 |
100 |
5,0 |
24 |
400 |
6,0 |
|
40 – 49 |
20 |
200 |
10,0 |
20 |
200 |
10,0 |
|
50 – 59 |
75 |
500 |
15,0 |
30 |
300 |
10,0 |
|
60 – 69 |
160 |
400 |
40,0 |
32 |
100 |
32,0 |
|
Cộng |
265 |
1300 |
20,4 |
126 |
1500 |
8,4 |
Từ bảng 4.1 ta thấy: Có sự không tương đồng về cấu trúc tuổi giữa 2 quần thể: Số người từ 40 tuổi trở lên ở quần thể A là 1.100 người, trong khi ở quần thể B: 600 người. Ngược lại, ở nhóm dưới 40 tuổi: quần thể A chỉ có 200 người, trong khi quần thể B có 900 người. Như vậy quần thể A có nhiều người cao tuổi hơn so với quần thể B.
Và nếu chỉ nhìn kết quả cuối cùng, khi so sánh tỷ lệ chết vì xơ gan ở nhóm có và không uống rượu, ta thấy tỷ lệ này gấp 2,5 lần (20,4/8,4). Đây là kết quả chưa chuẩn hóa.
Bây giờ ta sẽ chuẩn hóa tỷ lệ và lấy một trong hai quần thể làm chuẩn. Ví dụ lấy quần thể A làm chuẩn (lấy cấu trúc tuổi của quần thể A làm chuẩn), ta có bảng 4.2
Bảng 4.2: Số chết vì xơ gan ở quần thể B được chuẩn hóa theo cấu trúc tuổi của quần thể A
|
Nhóm tuổi |
Dân số quần thể A |
Tỷ lệ chết ở quần thể B |
Số chết giả định ở quần thể B theo cấu trúc tuổi của quần thể A |
|
20 – 29 |
100 |
4,0 |
0,04 x 100 = 4 người |
|
30 – 39 |
100 |
6,0 |
0,06 x 100 = 6 người |
|
40 – 49 |
200 |
10,0 |
0,1 x 200 = 20 người |
|
50 – 59 |
500 |
10,0 |
0,1 x 500 = 50 người |
|
60 – 69 |
400 |
32,0 |
0,32 x 400 = 128 người |
|
Cộng |
1300 |
|
208 người |
Từ kết quả bảng 4.2, khi lấy cấu trúc dân số quần thể A làm chuẩn (với tổng số 1300 người) thì số chết giả định ở quần thể B sẽ là 208 người. Như vậy, tỷ lệ chết chuẩn hóa theo tuổi ở quần thể B (theo cấu trúc tuổi của quần thể A) là: 16% (208/1300).
Sau khi đã chuẩn hóa, tỷ lệ chết vì xơ gan ở nhóm uống rượu (20,4%) so với nhóm không uống rượu (16,0%) chỉ gấp 1,2 lần (20,4/16,0) chứ không phải gấp 2,5 lần (20,4/8,4) như khi chưa chuẩn hóa.
Ý nghĩa
Tỷ lệ mới mắc
Đánh giá thực trạng sức khỏe cộng đồng ở một thời khoảng nào đó.
Là một chỉ số rất quan trọng trong việc xác định nhu cầu phòng bệnh và chữa bệnh cho cộng đồng, rất có ích cho cả các bệnh cấp tính và mãn tính.
Đánh giá hiệu quả của các biện pháp phòng chống dịch đã thực hiện cho cộng đồng.
Đánh giá và chứng minh vai trò của các yếu tố nguy cơ có mặt trong cộng đồng. Khi loại bỏ (hoặc làm giảm bớt) yếu tố nguy cơ nghi ngờ ra khỏi cộng đồng, nếu:
Tỷ lệ mới mắc giảm đi thì chứng tỏ yếu tố đó có liên quan đến bệnh;
Tỷ lệ mới mắc không thay đổi chứng tỏ yếu tố nghi ngờ đó không có liên quan tới bệnh;
Và nếu tỷ lệ mới mắc tăng lên thì yếu tố nghi ngờ không những không phải là yếu tố nguy cơ mà còn là yếu tố bảo vệ.
Tỷ lệ hiện mắc
Đánh giá thực trạng sức khỏe cộng đồng tại một thời điểm hoặc một thời khoảng nào đó.
Là căn cứ để lập các dự án, chương trình chăm sóc sức khỏe cộng đồng (số cán bộ y tế, số giường bệnh, thuốc và trang bị vật tư y tế…).
Ứng dụng trong việc tính cỡ mẫu sẽ nhanh chóng và sát hợp nếu căn cứ vào tỷ lệ hiện mắc.
Tỷ lệ chết
Đánh giá thực trạng sức khỏe cộng đồng.
Đánh giá nhu cầu khám chữa bệnh của cộng đồng.
Xác định ưu tiên cho các chương trình hành động: Bệnh nào gây tử vong nhiều sẽ được ưu tiên đầu tư nguồn lực nhiều hơn.
Xây dựng và củng cố hệ thống y tế phục vụ cho chăm sóc sức khỏe cộng đồng.
Xếp loại tầm quan trọng của bệnh.
Đánh giá hiệu quả của các chương trình can thiệp, dự phòng.